Neural-Network-Based Detection Methods for Color, Sharpness, and Geometry Artifacts in Stereoscopic and VR180 Videos
S. Lavrushkin, K. Kozhemyakov and D. Vatolin
Contact us:
Abstract
Shooting video in 3D format can introduce stereoscopic artifacts, potentially causing viewers visual discomfort. In this work, we consider three common stereoscopic artifacts: color mismatch, sharpness mismatch, and geometric distortion. This paper introduces two neural network based methods for simultaneous color and sharpness mismatch estimation, as well as for estimating geometric distortions. To train these networks we prepared large datasets based on frames from full length stereoscopic movies and compared the results with methods that previously served in analyses of full length stereoscopic movies. We used our proposed methods to analyze 100 videos in VR180 format — a new format for stereoscopic videos in virtual reality (VR). This work presents overall results for these videos along with several examples of detected problems.
Key Features
- 2 neural network based models for estimating 3 types of stereoscopic artifacts in VR180 videos
- Simultaneously detecting color and sharpness mismatch between stereoscopic video views
- 9,488 stereopairs of size 960 × 540 from 16 stereoscopic movies to train method for color and sharpness mismatch estimation
- 22800 stereopairs with artificial distortions from 39 3D movies in the train dataset for geometry mismatch estimation method
- Objective quality assessment of 100 VR180 videos from YouTube using proposed methods
Method for Color and Sharpness Mismatch Estimation
Train Dataset
The picture below shows an example with distortions added by the proposed distortion model.
A left view with generated color and sharpness distortions and an interpolated right view. The scene is from Captain
America: The First Avenger.
Architecture
Below is the general scheme of the proposed method for detecting color and sharpness mismatch between stereoscopic views.
Next the neural network architecture itself for which modified GridNet network [7] was chosen as the basis.
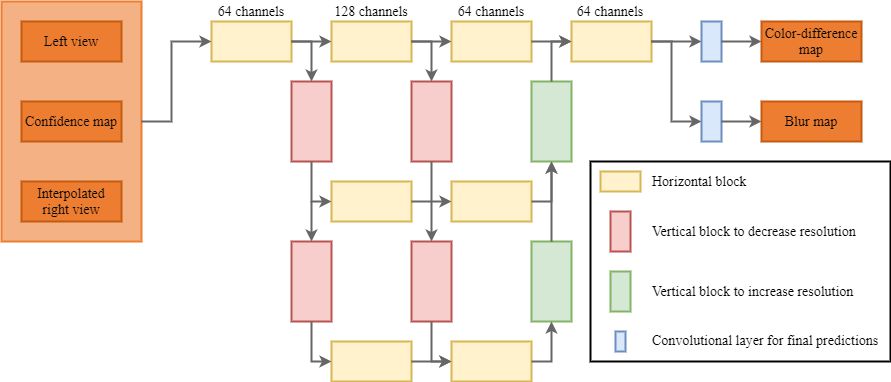
Training
- Loss function for predicting both color and sharpness difference maps was the sum of squared differences between the predicted and groundtruth values, weighted by the disparity map confidence and \(L_{2}\) regularization
- We set the learning rate to \(10^{−4}\), decreasing it by a factor of 10 every 40 epochs
- The batch size was 8, and the resolution of the training examples was 256 × 256
- The neural network training took place over 100 epochs
- Adam as an optimization method
Loss Function
\(L(\hat{c},c,\hat{d},d,\theta) = L_{c}(\hat{c},c) + L_{d}(\hat{d},d) + L_{2}(\theta)\),
\(L_{c}(\hat{c},c) = \frac{ \displaystyle\sum_{i=1}^{n} conf_i × ((\hat{c}_i^Y - c_i^Y)^2 + (\hat{c}_i^U - c_i^U)^2 + (\hat{c}_i^V - c_i^V)^2) }{3\displaystyle\sum_{i=1}^n conf_{i}}\),
\(L_{d}(\hat{d},d) = \frac{ \displaystyle\sum_{i=1}^n conf_{i} × (\hat{d}_i - d_i)^2 }{\displaystyle\sum_{i=1}^n conf_{i}}\),
where \(\hat{c}\) and c are the predicted and ground truth color difference maps, respectively, for each YUV color channel; \(\hat{d}\) and d are the predicted and ground truth blur maps, respectively; conf is the input disparity confidence map for the neural network; and n is the number of pixels in the image; \(\theta\) is the vector of neural network weights.
Results
Test dataset contains 23 stereoscopic video sequences with a resolution of 1024 × 436. Artificial distortions were added for each sequence based on the aforementioned general distortion model.
Table below presents the results.
| Method | PCC | SROCC |
|---|---|---|
| Color mismatch | ||
| MAE | 0.1254 | 0.1626 |
| MAE with right view interpolation | 0.1338 | 0.2039 |
| Winkler [1] | -0.4430 | -0.4093 |
| VQMT3D [4,10] | 0.8136 | 0.8760 |
| Proposed method | 0.9696 | 0.9602 |
| Sharpness mismatch | ||
| MAE | 0.1482 | 0.2635 |
| MAE with right view interpolation | 0.2683 | 0.3505 |
| VQMT3D [4,10] | 0.7686 | 0.6815 |
| Proposed method | 0.9762 | 0.9078 |
Method for Geometry Mismatch Estimation
Train and Test Datasets
Geometric distortions between stereoscopic views often occur in 3D shooting. The most common types include vertical shift, rotation, and scaling. We evaluated the geometric distortions between views in a stereoscopic movie wtih the VQMT3D project’s geometric distortion detection, then we computed the standard deviation for each distortion type and gathered only those stereopairs for which all three of these parameters had absolute values less than \(^σ/_{10}\).
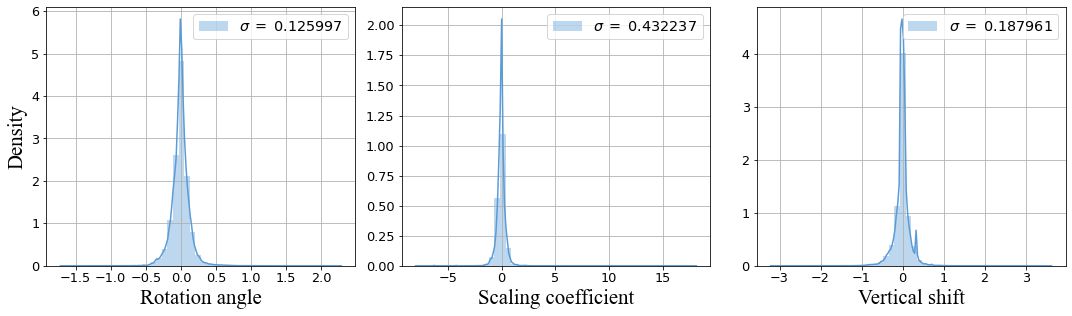Distributions of and computed standard deviations for the geometric distortions for thirty nine 3D movies.
Architecture
Below is the general scheme of proposed method for detecting geometry mismatch between stereoscopic views.
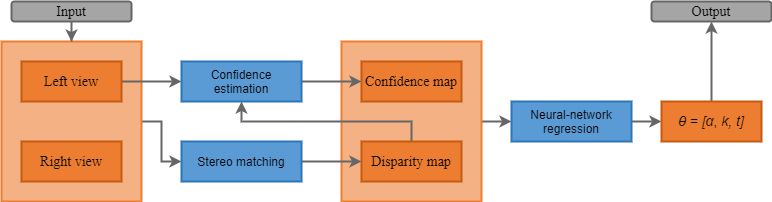
To estimate the geometry mismatch parameters we employ a neural network architecture, similar to ResNet-18 [6].
Training
- The proposed loss function includes three main terms:
- Squared difference between the predicted and ground truth distortion parameters
- Loss between two grids transformed using the predicted and ground truth affine transformations
- Measurement of the consistency between the neural network’s predictions of the disparity and confidence maps for the left and right views
- The neural network training took place over 120 epochs
- Adam as an optimization method
- Learning rate was \(10^{−4}\)
Loss Function
\(L(\theta,\theta_{gt},\theta_b) = L_{SE}(\theta,\theta_{gt}) + L_{Grid}(\theta,\theta_{gt}) + L_{Siam}(\theta,\theta_b)\),
where \(\theta\) is the neural network’s prediciton based on the disparity and confidence maps for the left view, \(\theta_{gt}\) is the vector of ground truth distortion parameters, and \(\theta_b\) is the neural network’s prediction based on the disparity and confidence maps for the right view;
\(L_{SE}(\theta,\theta_{gt}) = \omega_{SE}^{\alpha}(\alpha - \alpha_{gt})^2 + \omega_{SE}^k(k - k_{gt})^2 + \omega_{SE}^t(t - t_{gt})^2\);
\(L_{Grid} = \omega_{Grid}^{\alpha}MSE(G^{\alpha},G_{gt}^{\alpha}) + \omega_{Grid}^{k}MSE(G^k,G_{gt}^k) + \omega_{Grid}^{t}MSE(G^t,G_{gt}^t)\),
\(G^\alpha = T(G,\theta^\alpha), G_{gt}^\alpha = T(G,\theta_{gt}^\alpha)\),
\(G^k = T(G^\alpha,\theta^k), G_{gt}^k = T(G_{gt}^\alpha,\theta_{gt}^k)\),
\(G^t = T(G^k,\theta^t), G_{gt}^t = T(G_{gt}^k,\theta_{gt}^t)\),
where \(G \in R^{H×W×3}\) denote homogeneous coordinates of points on the plane, \(\theta^\alpha = \left[\alpha\quad0\quad0\right]\), \(\theta^k=\left[0\quad k\quad0\right]\) and \(\theta^t=\left[0\quad0\quad t\right]\);
\(L_{Siam}(\theta,\theta_b) = L_{SE}(\theta, -1\cdot\theta_b)\).
Results
Table below shows the absolute error for each geometric distortion. “No model” predicts zero for each geometric distortion.
| Method | Rotation angle |
Scaling coefficient |
Vertical shift |
|---|---|---|---|
| No model | 0.63406 | 0.6507 | 0.57497 |
| Yi et al. [2] | 0.05115 | 0.10810 | 0.19109 |
| Rocco et al. [3] | 0.43735 | 1.23582 | 0.82534 |
| VQMT3D [4,10] | 0.01158 | 0.02622 | 0.02004 |
| Proposed method | 0.01029 | 0.02071 | 0.00947 |
Cite us
@INPROCEEDINGS{9376385,
author={Lavrushkin, Sergey and Kozhemyakov, Konstantin and Vatolin, Dmitriy},
booktitle={2020 International Conference on 3D Immersion (IC3D)},
title={Neural-Network-Based Detection Methods for Color, Sharpness, and Geometry Artifacts in Stereoscopic and VR180 Videos},
year={2020},
volume={},
number={},
pages={1-8},
doi={10.1109/IC3D51119.2020.9376385}}Contact us
For questions and propositions, please contact us: sergey.lavrushkin@graphics.cs.msu.ru, 3dmovietest@graphics.cs.msu.ru, and video@compression.ru
See also
- Video Quality Measurement Tool 3D
- Stereoscopic Quality Assessment of 1,000 VR180 Videos Using 8 Metrics
- Stereoscopic Dataset from A Video Game: Detecting Converged Axes and Perspective Distortions in S3D Videos
- MSU benchmarks
- All MSU Stereo Quality Reports
References
1) S. Winkler, “Efficient measurement of stereoscopic 3D video content issues,” in Image Quality and System Performance XI, vol. 9016, p. 90160Q, International Societyfor Optics and Photonics, 2014.
2) K. M. Yi, E. Trulls, Y. Ono, V. Lepetit, M. Salzmann, and P. Fua, “Learning to find good correspondences,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 2666–2674, 2018.
3) I. Rocco, R. Arandjelovic, and J. Sivic, “Convolutional neural network architecture for geometric matching,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 6148–6157, 2017.
4) D. Vatolin, A. Bokov, M. Erofeev, and V. Napadovsky, “Trends in S3D-movie quality evaluated on 105 films using 10 metrics,” Electronic Imaging, vol. 2016, no. 5, pp. 1–10, 2016.
5) D. Fourure, R. Emonet, E. Fromont, D. Muselet, A. Tremeau, and C. Wolf, “Residual conv-deconv grid network for semantic segmentation,” in 28th British Machine Vision Conference, 2017.
6) K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778, 2016.
7) D. Fourure, R. Emonet, E. Fromont, D. Muselet, A. Tremeau, and C. Wolf, “Residual conv-deconv grid network for semantic segmentation,” in 28th British Machine Vision Conference, 2017.
8) D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412.6980, 2014.
9) K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770–778, 2016.
10) VQMT3D available online: http://www.compression.ru/video/quality_measure/video_measurement_tool.html